320x100
사실 해당 주제를 어디에 넣어야 할지 잘 모르겠더라.
여러가지 짬뽕되어있어서.
근데, 결과적으론 시각적으로 보이는게 되니깐 matplotlib 섹션에 누적하려고 한다.
import numpy as np
# precision은 소수점 자리를 말하는 거고
# suppress는 과학적 표기법을 의미한다.
np.set_printoptions(precision = 2, suppress = True)# usecols = 1번 컬럼만 사용하겠다.
pop =np.loadtxt('SP500_pop.csv', delimiter = ',', usecols = 1)
pop
'''
array([ 4.69929763e-01, 1.14371386e-01, -4.10536897e-01, 4.61146607e-01,
5.44394762e-01, 1.74318967e-01, 6.63205538e-01, 4.85810987e-01,
3.07009306e-01, 7.02185527e-01, 2.25970807e-01, -1.22015334e-01,
1.40202374e-01, 1.09321663e-01, 4.16430212e-01, 1.24475791e-01,
'''
# 실제로 csv파일에 내장되어있던 값들도 이런 값들이였다.
# 하지만 # np.set_printoptions(precision = 2, suppress = True)
# 를 거치고나서는 0.22 이런식으로 간결하게 값이 바뀌었다.# 이걸 해주는 이유는 근본적으로 SP500_pop.csv의 1번컬럼 내용이 스탠다드 푸어스 500 상위 기업의 수익률을
# 표기해주는 것인데, 이것이 0.55 보다는 55% 라고 좀 더 가시적으로 와닿을 수 있도록 설정해주는 것이다.
pop = pop * 100pop.size
# 500## sample 2017 return for 50 companies
sample = np.loadtxt('sample.csv', delimiter = ',', usecols = 1)
sample
'''
array([ 0.42, 0.16, 0.48, 0.58, -0.03, 0.14, 0.17, 0.37, 0.34,
0.07, 0.1 , -0.01, 0.49, 0.11, 0.95, -0.12, 0.05, -0.07,
0.29, 0.71, 0.42, 0.38, -0.12, 0.24, 0.19, 0.25, -0. ,
0.89, -0.1 , 0.2 , 0.09, 0.38, 0.1 , 0.19, -0.13, 0.15,
0.24, 0.23, -0.09, 1.32, 0.12, 0.7 , 0.36, -0.01, 0.5 ,
0.26, 0.12, -0.09, -0.02, 0.7 ])
'''sample = sample * 100
sample.size
# 50for i in sample:
print(i in pop)
'''
True
True
True
True
True
True
True
True
True
True
True
True
True
True
...
'''# 벡터화
np.isin(sample, pop)
'''
array([ True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True])
'''## Visualizing Frequency Distributions with plt.hist()
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(precision = 2, suppress = True)pop
'''
array([ 46.99, 11.44, -41.05, 46.11, 54.44, 17.43, 66.32, 48.58,
30.7 , 70.22, 22.6 , -12.2 , 14.02, 10.93, 41.64, 12.45,
16.85, -6.8 , 26.12, -22.11, -8.77, -3.83, 8.59, 21.79,
-2.46, 48.57, 131.13, -17.15, 41.27, 24.31, -2.26, 58.41,
11.01, -9.35, 49.12, 41.26, 18.94, 52.76, 35. , 55.96,
143.44, 59.57, 56.51, 20.15, 29.42, -33.48, 14.09, 30.65,
'''plt.figure(figsize = (14,10))
plt.hist(pop, bins = 75)
plt.title('Absolute Frequencies - Population', fontsize =20)
plt.xlabel('Stock Returns 2017 (in %)', fontsize = 15)
plt.ylabel('Absolute Frequency', fontsize = 15)
plt.xticks(np.arange(-100, 401, 25))
plt.show()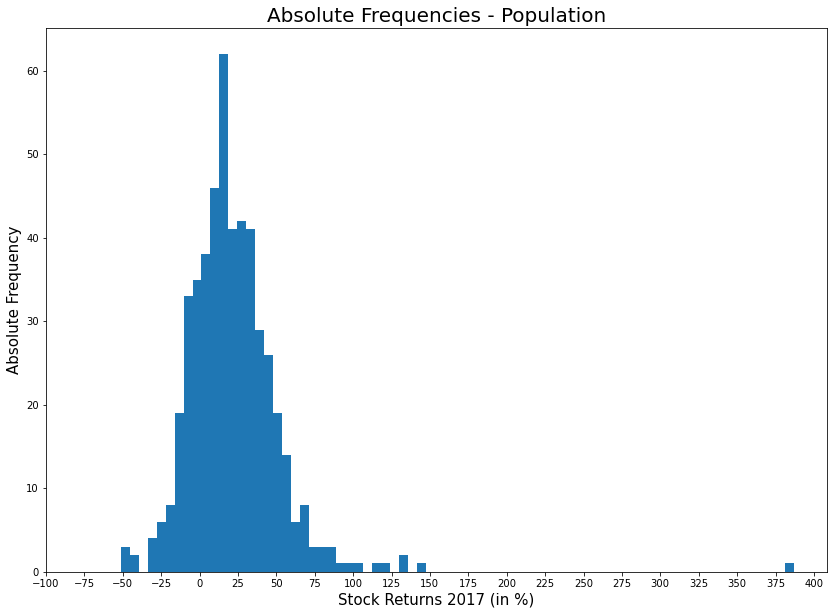
## Relative and Cumulative Frequencies with plt.hist()
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(precision = 4, suppress = True)(np.ones(len(pop))/ len(pop))
'''
array([0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002, 0.002,
0.002, 0.002, 0.002, 0.002, 0.002])
'''# 상대도수 그래프
plt.figure(figsize = (14,10))
plt.hist(pop, bins = 75, weights = np.ones(len(pop)) / len(pop))
plt.title('Relative Frequencies - Population', fontsize = 20)
plt.xlabel('Stock Returns 2017 (in %)', fontsize = 15)
plt.ylabel('Relative Frequency', fontsize = 15)
plt.show()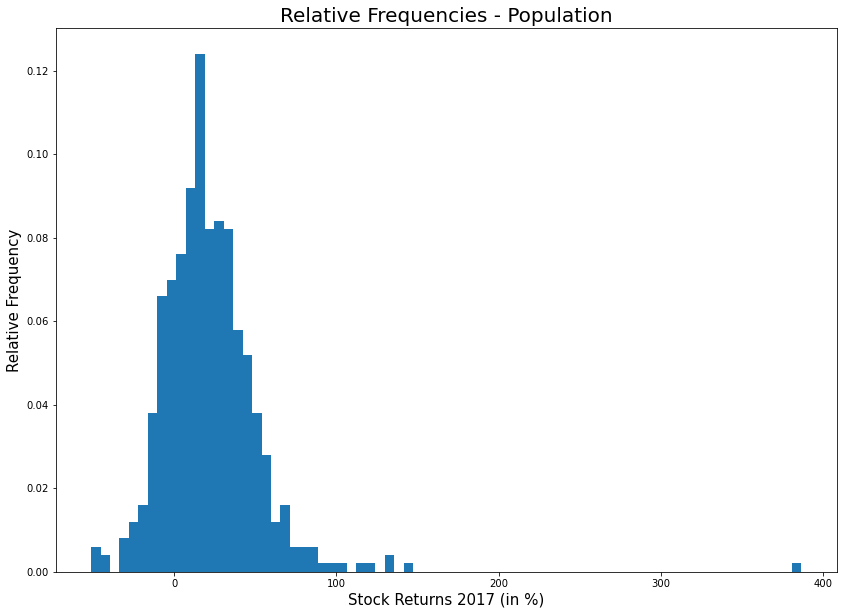
# y축의 값이 위의 상대도수 그래프와 비교해서 다르다.
plt.figure(figsize = (14,10))
plt.hist(pop, bins = 50, density = True)
plt.title('Relative Frequencies - Population', fontsize = 20)
plt.xlabel('Stock Returns 2017 (in %)', fontsize = 15)
plt.ylabel('Relative Frequency', fontsize = 15)
plt.show()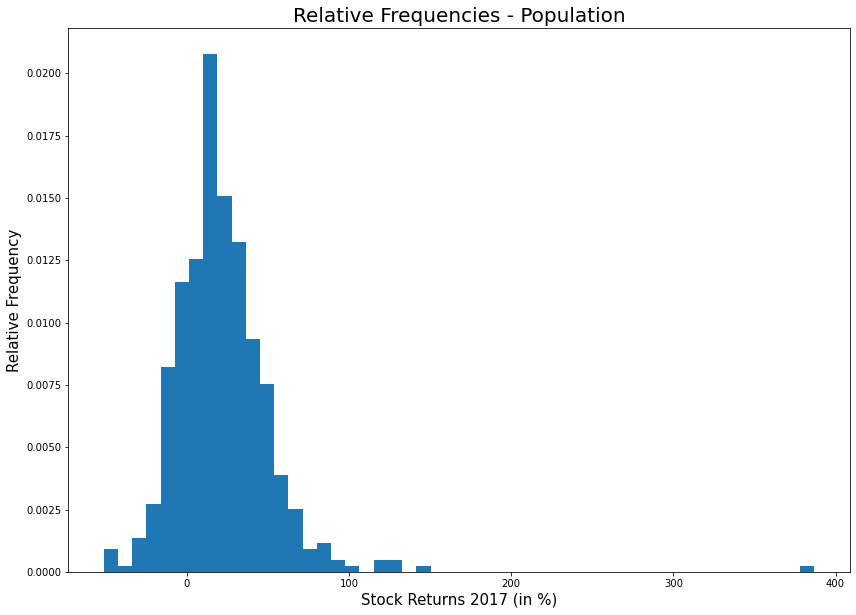
# 누적도수 그래프
plt.figure(figsize = (14,10))
# cumulative라는 뜻 자체가 '누적하는'이라는 뜻이다.
# density는 '밀도'
plt.hist(pop, bins = 50, density = False, cumulative = True)
plt.title('Cumulative Absolute Frequencies - Population', fontsize = 20)
plt.xlabel('Stock Returns 2017 (in %)', fontsize = 15)
plt.ylabel('Cumulative Absolute Frequency', fontsize = 15)
plt.show()
# 누적 상대도수 분포도
# 상대도수라서 최고 누적값이 1이 된다.
plt.figure(figsize = (14,10))
plt.hist(pop, bins = 50, density = True, cumulative = True)
plt.title('Cumulative Relative Frequencies - Population', fontsize = 20)
plt.xlabel('Stock Returns 2017 (in %)', fontsize = 15)
plt.ylabel('Cumulative Relative Frequency', fontsize = 15)
plt.show()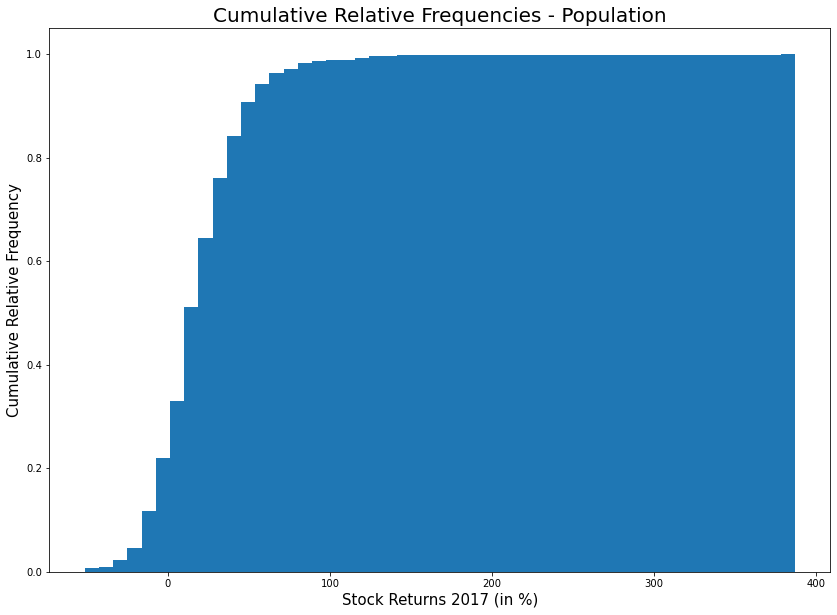
300x250
'개발일지 > 임시카테고리' 카테고리의 다른 글
| linux 기초1 기본 명령어, 옵션 (0) | 2022.08.26 |
|---|---|
| Linux 시작 전 (0) | 2022.08.26 |
| matplotlib 기초 그래프 구현의 원리 (0) | 2022.08.26 |
| python matplotlib ValueError: x and y must be the same size (0) | 2022.08.26 |
| SQL 기초 22 HAVING (GROUP BY와 셋트메뉴라고 보면 된다) (0) | 2022.08.25 |
